Underground drainage systems and geothermal flux
Badino, G.
Abstract: The paper presents an analysis of the interaction between the geothermal flux and the water or air- deep drainage networks. The problem of geothermal power intercepted by deep structures and, in general, the temperature field calculations, is converted to classical thermo-engineering problems in terms of shape factors. It is shown that the fluid flow in a conduit perturbs the whole deep rock temperature field until the geothermal flux of a large area is focalised onto the conduit. It is shown that either small water masses flowing into a mountain are able to perturb the rock temperature up to the surface, on sizes that do not depend on water mass dimension, but on its depth, and then on enormous volumes. The introduction of the ?geothermal cross section? of an underground drainage structure allows us to improve the classical formula of minimum provenance depth of geothermal water. Enlarging factors are applied to the classical estimation in dependence of the ratio between the actual average discharge and the critical discharge Qc, which depends on the conduit geothermal cross section. The geothermal ?umbra cones? created in the overlying rock by deep underground structures are described.
It is shown that the geothermal flux can play a significant role in the underground drainage phenomenology.
Keywords: geothermal flux, heat transfer in karst massifs
1. The geothermal flux and the energy contents of rocks
An introduction to the geothermal energy flux
It is widely known that the rocks below us have temperatures that increase with depth. The reason is that the internal part of Earth is hot and the surface cold; there are then two “heat sources” (but in this work I have adopted the suggestion of Bohren (Bohren, 1998), avoiding use of the word “heat”), and the thermal energy flows between them with the rules given by the usual conduction equations.
Table 1, adapted from (Lee, 1966) gives typical values, widely variable, of geothermal flux, estimated by measures of deep underground temperature gradients.
Table 1
Typical values of geothermal flux
Regions |
Mean geothermal flux Fgt |
Number of measures |
|
Continents |
||
|
Africa |
36-61 |
15 |
|
America |
25-150 |
85 |
|
Australia |
35-160 |
65 |
|
Asia |
22-150 |
60 |
|
Europe |
26-140 |
60 |
|
Oceans |
||
|
Atlantic |
3.4-250 |
250 |
|
Indian |
5.9-220 |
250 |
|
Pacific |
2.9-340 |
600 |
|
Arctic |
33-62 |
20 |
|
Geothermal regions |
||
|
Larderello (I) |
450 |
|
|
Oora Kei Korake (NZ) |
4200 |
|
|
Matsukawa (J) |
630 |
|
The world average (Verhoogen, 1956) is
![]()
The flux is some 60 kW per square kilometre, which corresponds to a total release of 3´1013 W on the whole planet. For comparison the energy flux received from the Sun is 1.7´1017 W, therefore the geothermal flux is around 5000 times smaller than the main energy source for Earth. It cannot play a role in the free atmosphere phenomenology, but we are going to see that in the case of underground atmospheres it can and it does.
At first, this appears not to be true in the case of cave atmospheres, that are really quite cold (essentially at the yearly average external temperature, -from hereafter Tave ; Badino, 2004) while the atmosphere of mines can be very hot (Badino and Forti, 2005). Actually the first aim of this work was to show that the geothermal flux could not play any role in the deep karst microclimates and genesis, because it is shielded by deep drainage conduits: This is exactly the contrary of what we are going to show...
Mines, caves and tunnels
The first point to discuss is the difference between the temperature of artificial and natural cavities in order to clarify the common confusion between “thermal flux” and “temperature”.
It is useful to compare two Underground Neutrino Observatories, in Mont Blanc (between France and Italy) and in Gran Sasso (in central Italy), which are assembled in halls in motorway tunnels. The depth of the first, dismissed in 2001, was some 1800 m below the surface, at an altitude of 1300 m asl, whilst the depth of the second is around 1050 m at an altitude of 1000 m asl. Their temperatures are nevertheless completely different, in the first it is around 32 °C, in the second at 6 °C, the two unsuitable for working. Therefore it is necessary to act in the opposite sense, in the first to cool, in the second to warm the experimental halls.
The reason for the two different temperatures is the different rock permeability.
The Mont Blanc rock is mainly granite, the waters met by the tunnel were essentially fossil waters, the meteoric water circulation being quite epidermal (up to depth of 100-200 m below the surface), with some exceptions localised along large major rock discontinuities.
The Gran Sasso rock is essentially limestone, and drillings have shown a cave layer 550 m above the tunnel altitude, and a general water table extended up to that level. The infiltration waters at the surface are essentially at Tave, and cross the whole mountain in nearly adiabatic conditions, which means that they are only very slowly heated along the fall. Therefore in the Mt Blanc’s depth there are essentially “mine” waters in thermal equilibrium with hot, deep rocks, whilst the deep Gran Sasso waters are essentially meteoric waters, in equilibrium with the atmosphere.
It is useful to discuss a little more the internal water heating in karst. The reason for water temperature increase during underground fall is the gravitational energy which is converted in thermal (a process that gives a water adiabatic lapse rate –2.34 °C km-1) and, in the case of flowing in vadose conditions, also to thermal exchanges with moist air, always characterised by a different adiabatic lapse rate, around -5 °C km-1. The actual caves’ lapse rates are between these two extremes (Badino, 2000; Luetscher and Jeannin, 2004), a fact that has huge consequences on the caves energetic balances, which nevertheless are outside this work aim; we return briefly to it in the next chapter, but a discussion can be found in (Badino, 2005). We concentrate here on the fact that the infiltrations create a thermal connection between the atmosphere and the deep karst.
In short the thermal contact between deep waters and atmosphere in the Mont Blanc case is due to the recent tunnel, in the Gran Sasso to the natural ancient conduits that have permitted a deep water flow that has been able to shield the geothermal flux from below and to cool the whole mountain above the water table.
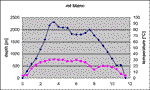
More in general we can compare the temperature in the bulk of large mountains looking at the temperatures encountered during the tunnels construction. The world’s deepest tunnels are essentially in the Alps and it is possible to discuss their internal temperatures. The figures, adapted from (Szechy, 1973) show the rock profile above the tunnels and the corresponding local temperature.
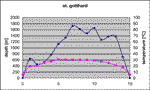
The first figure (Fig. 1) shows the situation of the St. Gotthard tunnel, in Switzerland, mainly in granite and gneiss. It is possible to see that the temperature dependence with depth is quite regular.
Fig. 1. Depth profile and rock temperatures in the St. Gotthard tunnel.
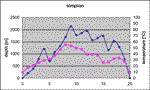
Next figure (Fig. 2) shows the situation in the Simplon tunnel (between Italy and Switzerland), a geological structure in gneiss and, roughly in the Italian part, limestones. It shows low temperature anomalies in the sedimentary part around PK 15 (Luetscher and Jeannin, 2004).
Fig. 2. Depth profile and rock temperatures in the Simplon tunnel.
The Mt Blanc situation is quite different (Fig. 3). Its rock is mainly protogine, but there is an important fault that allows very deep glacial water circulation, which has lowered the rock temperature near PK 8, where extreme excavation problems where encountered (Guichonnet, 1967). The general behaviour is regular, but the whole mountain has been cooled a little by the fault.
Fig. 3. Depth profile and rock temperatures in the Mont Blanc tunnel.
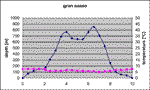
The next figure (Fig. 4) shows a completely different situation, the Gran Sasso (Catalano, 1993). Not only the temperature does not increase with depth, but also it shows a tendency to decrease with it, because as deep as it is, as colder are inflowing waters. We have seen above that they meet a very small warming crossing the mountain (Badino, 1995).
Fig. 4. Depth profile and rock temperatures in the Gran Sasso tunnel.
Other more complex phenomena can occur in determining the rock temperature. For example Szechy cites the case of the Great Appennine tunnel (Italy), mainly in limestone and clay, where a local temperature of 60 °C, 500 metres below the surface, has been encountered. The Author says that “discrepancies are due to intensive methane infiltration through the Eocene clay shale”, which looks quite strange. Nevertheless it is quite common to meet high temperatures connected with local thermal water infiltrations, often connected with hyperkarstic phenomena (Badino and Forti, 2005). Here we deal only with a “standard” situation to analyse the geothermal impact on our usual karst.
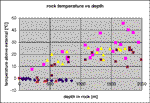
Convective mountains
The graphics (Fig. 5) show in short the above discussed data (temperature vs. depth) where each type of data point indicator describes a different tunnel. It is possible to see two completely different behaviours, the “hot” mountains without internal water fluxes, with positive temperature gradient, and the “karstic” mountains with slowly negative or zero gradients.
Fig. 5. Rock temperature versus depth in the large alpine tunnels.
In fact these mountains are in thermal contact, and in equilibrium, with the local climate, that they follow with a delay that depends on the mountain depth (Badino, 2004).
This thermal contact surface-underground due to water vein, is the base for the traditional and fundamental “remote sensing” during tunnel excavations. Continuous rock temperature measurements are performed during work (Guichonnet, 1967); a regular temperature increase with the surface distance is a signal of compact rock. Occasional water veins are in thermal equilibrium with geothermal flux, which is possible only if these water reservoirs are relatively small and without a hydro-geological connection on long ranges, and then cannot be extremely dangerous. Otherwise, if during excavation appears a tendency to a temperature reduction, it is a sure signal of an approaching water stream in direct contact with the surface, that at these depths has obviously enormous pressure, which is able to create extremely dangerous situations, also because it is surely associated to dramatic rock discontinuities. This is the reason why a lot of work is made in the field of rock temperature estimations in deep tunnels (Koenigsberg, 1906; Goy et al., 1996; Badino, unpubl. 2005).
Underground high temperatures are related to good thermal insulations, which means that a tunnel, or a mine, can be excavated across rocks that are very hot (high temperature) because, i) they have almost no contact with the surface and ii) they have then acquired equilibrium with the geothermal flux. Then the relative rock insulation has allowed to a so small thermal flux to heat up to high temperatures enormous quantities of matter.
As we have seen above, it is possible to consider mountains with caves as good thermal conductors and then in general (let us forget for a while the geothermalism) they are in thermal equilibrium with the external atmosphere.
As larger are the caves, as smaller it is the impedance for water crossing the whole mountain, then deep water circulation is possible and the whole structure is crossed, which is a big difference from a mountain without caves where only water circulation is quite epidermal.
Another consequence to be pointed out is that if the mountain is highly permeable to water fluxes the thermal energy transfers inside it are absolutely dominated by fluid motion, then the pure conductive terms into the rock (“heat” diffusion) become negligible.
It is possible to add that low-impedance water (or air) transfers inside a mountain can be considered a special case of thermal convective movements, and then the karstic mountains are examples of convective thermal contact with the atmosphere, whilst the impermeable rocks have only a conductive contact with it, with a very poor efficiency.
The hot mountains energy contents
Let us estimate the energy contents of a hot rock prism, with a surface A and an altitude of H. Its temperature at the beginning is T0=Tave, local average temperature.
The geothermal flux will heat the rock until the temperature gradient in it becomes able to evacuate the geothermal power on the surface. This equilibrium condition (“stationarity”, i.e. no time dependence) is obtained when the gradient is
![]()
Where we have used partial derivative because in general the temperature is function also of time. This is exactly the condition that allows the measure of geothermal flux from temperature gradient data, assuming a steady-state condition.
In this case we can assume a rock thermal conductivity KR=2.5 Wm-1 K-1, typical for granite, whilst the limestone conductivity is some 10% less. Then the temperature gradient at the equilibrium is
![]()
Which is 24 °C per kilometre. It is easy to calculate the energy necessary to heat at this constant temperature gradient a rock prism of surface A from depth Z up to the surface; its total available energy is
![]()
Where CR is the rock specific thermal capacity (800 J kg-1K-1) and rR its density (roughly 2600 kg m-3). For example, assuming Z=1 km, with typical values the total energy contents per kilometre square of surface is
![]()
For comparison, a 20 kTon atomic bomb yields 1014 J.
It is important to note that this energy, that a power plant of 1 GW produces in two years, has been released to our prism rock by the small geothermal heater, only 60 kW. It is a small power, but it has worked from a very long time, the rock is a very efficient thermal insulator and the final result is an efficient energy storage.
Rock heating time
To estimate correctly the time needed for heating, it is necessary to take into account that the rock prism is in contact with others all around; the calculation would have to include these in the estimation, reconstructing the whole temperature field and its dependence on time. The problem is complex but we can do a crude estimation of the prism heating time scale considering it as thermally isolated from its surroundings (which is equivalent to assume a flat surface and uniform, uni-dimensional heating), then
![]()
The last term can be rewritten in terms of thermal diffusivity coefficient defined as
![]()
In the case of rock
![]()
And then
![]()
Typical width of limestone mountains are around 1000 m, then the heating time scale is around 104 years, not so much for geological time scale, but longer than the typical global climate fluctuation (Badino, 2004).
Penetration lengths of temperature fluctuations
Let us recall the classical thermal fields solution of a homogeneous thermal conductor to a sinusoidal and to a sudden (step) temperature change.
In the first case a thermal wave propagates inside, fading exponentially (Badino, 2004; Lismonde, 2002). If tsin is the period of sinusoidal wave we have that the “penetration length” is
![]()
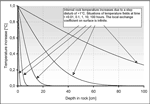
If the temperature fluctuation has a step shape, the propagation length is more difficult to define. The penetration of thermal shock of amplitude ∆T is described in terms of rock temperature increase at depth x at time t, by equation (Isachenko, 1969)
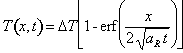
Where erf(u) is the Error Function. The figure (Fig. 6) shows the results at different times. A discussion about the properties of this solution can be found in (Lismonde, 2002).
Fig. 6. Diffusion in rock of one step temperature increase on its surface.
The last equation suggests that a step thermal wave is able to reach a depth x in a time t or, vice versa, after a time t the thermal disturbance has reached the depth x, and the relation between the two quantities is given by the argument of Error Function. More precisely it is possible to show (for example, classically (Laidler and Meiser, 1995) that
![]()
Then the penetration in rock up to depth Z of a cool wave requires a time-scale Dtcool
![]()
The estimation is heavily approximated, because we are not looking for the complete cooling of the mountain, but for the equilibrium temperature field formation inside it, what is attained not when the whole rock is at the same temperature of the surface, but when its temperature has attained the “stationary temperature field” geothermal gradient seen in the previous chapter. Nevertheless it makes no sense to try to perform exact calculations, which in any case work with unrealistic forms of mountain.
We can conclude that the heating and the cooling time-scale up to the equilibrium configuration are almost the same, and they do not depend on the temperature drop, then at depth Z in metres we have
![]() [1.1]
[1.1]
In the case of compact rock we can assume that the equilibration time scale in years is given by
![]()
This estimation is very important for our discussion. In the next chapters we are going to consider water and geothermal fluxes that have attained stationary conditions. It is then obvious that if the water flow has begun from a time that is much smaller than that of equilibration time, it is not possible to assume that the system has attained a general equilibrium configuration, what in fact happens in the artificial excavations. This is the reason why the mines are hot.
2. The basic approach to the problem
The problem of infiltration temperature
The classical Desio’s formula (Celico, 1986) that gives the minimum depth attained by geothermal water is based on the assumption that underground there exists a first layer (heterotermic) in thermal contact with the atmosphere with essentially the temperature of local inflowing fluids, which have a temperature T0 quite precisely (but in general, a little lower, (Badino, 2004)) equal to the local yearly temperature Tave. Below this first layer the rock temperature increases in conductive regime (homotermic region).
The heterotermic layer is also called “active layer” (US Bureau of Mines, 1996), mainly because the seasonal variations can create icing.
It is necessary to note, nevertheless, that some problems do exist in the definition of homotermic layer (Schoeller, 1962; Celico, 1986), because it is considered the layer where temperature does not depend on atmospheric temperature variations, not the layer where temperature is equal to the local average of the atmosphere. It is then defined on the basis of its temperature stability, not on the basis of its thermal contact, if with atmosphere or with deep rocks. Really in rock with deep aquifers we meet a heterotermic layer with seasonal fluctuations (some score of metres), a layer above the aquifer (included) at T0 (Luetscher, 2004; Badino, 2005), a thin layer of thermal contact deep rocks-aquifer, where a relatively sudden temperature increase, probably dependent of aquifer permeability, is possible (Goy, 1996; Badino, unpubl. 2005). We would call it the “geothermal exchange layer”. Below this region, a regular temperature increase in deep rocks is found. The scenario is then more complex, but it is better to postpone a detailed discussion to a future work.
We can spend some words about the exact value of T0 and its relation with Tave. Really Tave depends on the altitude, and on average decreases of 6-6.5°C per kilometre, as described with the International Standard Atmosphere. Also at a first approach it looks better to think that the rock assumes not the average yearly temperature of the atmosphere Tave, but the average temperature of waters at the infiltration point, that is quite lower because the rain waters in alpine karst are generally associated with colder periods (but in tropics with warmer periods); really, many other corrections are necessary to estimate the local rock temperatures (Badino, 2004).
Another corrective term, already cited above, appears during the underground flow because the temperature increase of underground waters along their travel is different from outside, where the waters follow the ISA mean lapse rate (6 °C per kilometre of fall). Underground, in adiabatic conditions the theoretical value of water temperature increase is 2.34°C per kilometre of fall, but the experimental values into the caves, where energy exchanges with the air are possible, are around -3 and -4°C km-1. Really, we can assume that the water temperature that has infiltrated at altitude H [km], when it arrives at level 0 is some (3-4)´H [°C] hotter, then sensibly colder than the corresponding infiltrating waters at that altitude.
In detailed calculations these effects, that create a difference between the actual cave temperature T0 and the local yearly temperature at its same altitude Tave, have to be taken into account, but in our discussion they are completely negligible.
The energy release to groundwater
There is an obvious approach to consider the role of geothermal flux.
In the upper Earth surface layers the geothermal energy is essentially intercepted by water that releases it to the atmosphere when it goes out from springs.
The energy that comes onto a large surface A is obviously FgtA, and it is very regular in time. Let us suppose that it is absorbed by a mass M: Its temperature increase rate is then given by the condition
![]()
Where Cw is the water thermal capacity, that is
![]()
Then if we know the shielding mass M we can calculate its temperature variation with time, but how large is M? Reasonably it is the mass of groundwater, but it changes seasonally, depends on rock characteristics and so on. Still worse, the previous equation says that the temperature continues to increase because the mass is stable and the energy flux continues. The equation gives us a temperature-changing rate, not a temperature variation.
It is easy to avoid these problems. Really the mass M can change, but its water is almost continuously flowing, which means that some water enters cold in the mass M, and on average the same quantity flows away from some other side, warmer. We will impose a condition of steady state and calculate the temperature variation of the flowing water, independently on M and, above all, on time.
The geothermal energy flux is very regular but the groundwater flow in general it is not. We then may expect that the temperature change fluctuates, also if we consider the over-simplified system of a single water mass M and we neglect other problems like the drainage network structure and mixtures between different branches that depend on the water flow rate.
So, the temperature changes fluctuate, but we are going to estimate the average value of temperature increase due to geothermal flux.
The groundwater temperature increase
It is easy to estimate the flowing water temperature increase, assuming the powerful and reasonable hypothesis that on average the system is stationary. This means that the thermal energy inflowing in M from Earth is, on average, going out as water flux enthalpy increase. In this way we have not to consider the mass M, that we cannot know, but only the outgoing flux from it, because our steady state assumption states also that the temperature of M does not change with time (on average...).
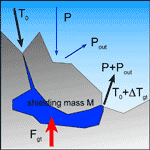
Let us estimate the water flux out-flowing from a region of surface A, which thermally interact underground. If the precipitation is P (in kg m-2s-1), the infiltration is P minus the part Pout “lost” outside due to evaporation. This part depends on climate, surface type and so on; in temperate regions ranges between 30 and 40% of total, but in deserts can rise to 90% (Celico, 1986). With this assumption the enthalpy extracted from the system is (P-Pout)DTgtA, where ΔTgt is the water temperature increase during deep flow (Fig. 7). The condition of stationarity implies that on average the temperature cannot change in time and then
![]()
That solves our problem. We can change units, calling P* the infiltration in [mm a-1], to obtain
![]() [2.1]
[2.1]
Fig. 7. Interception of geothermal energy flux by a flat aquifer. In stationary approximation the water is heated and the upper rocks are completely shielded.
The upper parts of drainage systems (for instance the caves, highly permeable) are almost exactly at the external average local temperature, therefore the water is in general warmed of DTgt between the lowest cave parts and the springs, that is along the flow in the phreatic systems.
In alpine karsts P* is some 1000 mm a-1 and then the water average temperature increase due to geothermal energy is some 0.5°C.
It is a small term, very difficult to measure, and really it has never been measured. But it is not always so small, a temperature increase of 5°C between the caves and the springs has been measured in Cuatro Ciénegas, a figure that corresponds to an infiltration (P*-Pout)=100 mm a-1 in this desert region of Coahuila, Mexico (AA. VV., 2004).
Therefore it would theoretically be possible to estimate the average infiltrating flow measuring this temperature increase, but it is a measure quite difficult to do with some accuracy, because it is the difference of two uncertain parameters, and other processes surely occur along the water rock crossing.
The plane watertable
We have used these calculations in a previous work (Badino, 1995) to explain why the karstic mountains are so cold, therefore excluding a significant role of geothermal flux in underground climate definition, because the energy flow from Earth depths is easily shielded. This very natural approach to refuse, in general, any role to the geothermal flux, it was not original, it is a quite traditional point of view.
Bögli (Bogli, 1980) estimates reasonably 0.2 °C “to prevent the karstified zone above from being geo-thermally heated up”, that is a very interesting idea that we shall meet again. In a very interesting and complete paper Mathey (Mathey, 1974) estimates a maximum of 0.55 °C. More recently Jeannin et al. (1997) estimate the specific discharge of a karstic spring (the equivalent of infiltration) between 30 and 3000 mm a-1. The first figure seems too low (almost three times dryer than the North Mexico deserts), but in this paper it is used an energy flux too low by a factor thousand, to finish to say that the temperature increase, that has physical dimension [°C], is “less than 0.1 °C/a”, where really the 30 mm a-1 case would be warmed by some 15 °C.
Let us return to this estimation. We have obtained the average water temperature increase and we could now begin to calculate the fluctuations dependence on discharge and so on. But we are dealing with conduits, not with plane watertables. Are these calculations and assumptions true for similar “discrete” systems? The general answer is that no, they are not generally correct.
The water flows along definite branches, that do not cover a large surface and with a general shape that is far from regular. The complete shielding assumption is not reasonable for karstic drainage.
3. The underground temperature field with a drainage network
The problem
The scenario described above (a regular, flat, diffuse water table) can sometimes be correct but in general it gives completely wrong results in the internal rock temperature field estimations.
To study a more real model it is necessary to estimate the energy interception made by a system (a thermodynamical sink) that is buried in a semi-infinite medium where a thermal energy flux is flowing from infinite.
Let us consider the problem details.
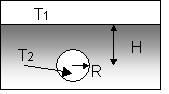
We have a semi-infinite rock volume in which a thermal flux Fgt is coming from below. It creates a temperature gradient given by:
![]()
Where we have assumed the depth z as positive downwards. The temperature field at depth H below the surface (or, better, below the heterotermic layer) it is therefore given by
![]()
We have previously seen that T0 is essentially the local Tave. It is very natural to suppose that the geothermal energy intercepted by a deep structure is that given in previous chapters, that is (geothermal flux)´(structure area), therefore
![]() [3.1]
[3.1]
This means that the energy intercepted by a “cave” is proportional to its surface in the direction of energy flux. It is a very natural assumption, but it is false.
The fact that, up to now, has not been considered is this: If we bury a system able to intercept and to evacuate elsewhere the energy, the whole temperature field in the rock is altered and then the flux itself changes.
The geothermal field with a cave
The problem of temperature field calculation in this configuration has to be solved with these boundary conditions:
1) The geothermal flux from infinite is constant, Fgt;
2) The temperature on the surface is T0 constant everywhere;
3) The cave temperature is T0, the same as on the surface (we have sufficiently discussed the limits of this assumption);
4) At the infinite the temperature field is not disturbed by the cave existence.
These conditions imply a flat external topography and assume that the infiltrated water heating from surface to the cave is negligible.
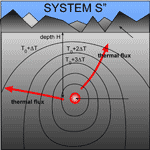
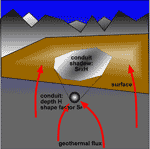
We said that if the cave has an area A, it is natural to assume that the absorbed geothermal energy is Fgt´A [Eq 3.1]. Is this correct? Let us firstly discuss it qualitatively, drawing the isothermal surfaces in the rock. The figure (Fig. 8) shows a reasonable situation that respects the boundary conditions. It is possible to see two things:
1) The isothermal surfaces have a tendency to converge, then to be focussed, onto the cave;
2) They are “compressed” around the cave.
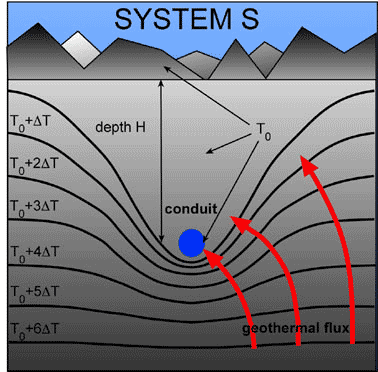
Fig. 8. Qualitative view of the stationary thermal field due to the interaction between the geothermal flux and a conduit with strong drainage (system S). The isothermal surfaces are affected in a wide region, and the cave temperature is T0.
If we remember that the thermal flux flows along the maximum T variation (i.e. along the grad (T), which means perpendicularly to the isothermal surfaces) and that its value is proportional to the gradient of T, we have that the two features are equivalent to say that: i) the cave focus on itself the geothermal flux and, ii) in the rock surrounding the cave the geothermal flux (and the geothermal gradient) is much more intense than the natural one...
So, the assumption that gave us the [Eq. 3.1] is surely wrong.
But is it possible to calculate the correct value? Quite surprisingly it seems that nobody has studied this important problem.
Before we look for the solution, we have to make some note about the enormous weight of the stationarity assumption. Whatever initial temperature field condition will converge to asymptotic values which are solution of Laplace equation, but this convergence requires time. During this time, which is of the order of equilibration time scale introduced above [Eq. 1.1], the difference between the real field (in transient phase) and the asympotic one (stationary phase) can be important. If the equilibration time is comparable with the typical changes of boundary conditions (global climatic changes, infiltration of hot waters or so on), the system can never be considered in a true stationary phase, and the equation given by this assumption has to be considered heavily approximated. This limit of stationary assumption gives strong uncertainty in the temperature fields estimations for the new deep alpine tunnels, which have very long equilibration times (Badino, unpubl. 2005), and affects also our next considerations.
The general solution
Therefore the problem of calculation of stationary temperature fields is very difficult to solve just with the easy boundary conditions given in the previous chapter. What to expect, then, when we will have to assume finite energy transfer rate inside the cave or situations in which the temperature of the cave itself is determined by the geothermal flux? And what monstrous form may assume the solution in a non-stationary case, if we want to consider, for instance, the cooling of a mountain during the karst creation inside it?
Nevertheless there is a simple way to lead this problem to typical situations of engineering thermal exchange.
Let us show how, considering three different systems, S, S’ and S”:
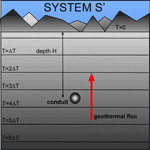
1) The main system just now described, the real case, which we call from hereafter S (Fig. 8);
2) The system composed only of semi-infinite undisturbed rock, without caves and with external temperature equal to 0, which we call from hereafter S’ (Fig. 9);
3) The more complex system S”, (Fig. 10), composed by a cave at a particular temperature T” buried in a semi-infinite rock, that releases energy to the surface at temperature T0. Also the rock at the infinite is assumed to have temperature T0. In this last ideal system S” there is no geothermal flux at all.
Fig. 9. Qualitative view of the stationary thermal field due to the interaction between the geothermal flux and a conduit with no drainage (system S’). The isothermal surfaces are unaffected, and the cave temperature is higher than T0.
Fig. 10. Qualitative view of the stationary thermal field between a “hot conduit” at temperature T” and the surface at T0 (system S”). The isothermal surfaces are finite, closed and contain the conduit. Heat diffusion problems like this one are quite usual in thermal exchanges engineering.
We are then ready to do the final step, assuming that T” in S” has a value given by:
![]() [3.2]
[3.2]
where H is the cave depth from the surface. We then assume that the cave in S” has exactly the temperature of the rock at depth H in the system S’ plus T0.
Let us consider now the three temperature fields. They are the solution of general Fourier equation (Isachenko, 1969)
![]()
That in our case, not time dependent, it reduces to the Laplace equation
![]()
It means that the T fields behave like a huge class of phenomena for which the sum of the three spatial second derivatives is zero. The functions that satisfy these conditions are called “Harmonic Functions”, and are among the most important and studied functions in Physics (Carslaw and Jaeger, 1959; Bejan, 1993; Balcerzak and Raynor, 1961; Nashchokin, 1979). By the way, it would be possible to solve our fields using solutions given for different and well-studied problems like, for instance, the electric field due to particular charge distributions, but we can do better for our purpose.
The field structure around S, that we have qualitatively shown (Fig. 8), is our unknown term.
The field structure of the second S’ it is obvious, it is composed by many horizontal parallel lines (or planes, in 3-d) for T-field and vertical vectors for thermal fluxes.
The third system is the most exciting. There are almost no lines all around (neither for T nor for thermal fluxes) unless in the region between the cave and the surface, because the temperature difference between the “hot cave” and the surface and also the “infinite”, drives an energy flux. From the other side, this situation is a very usual situation for engineering, because the “hot cave” can be a tube transporting hot fluid buried in some engine...
Now we can do the last step: We state that the unknown T field of the system S is given by
![]() [3.3]
[3.3]
That is, we can subtract the (very complex, but very common) T” field from the trivial T’ to obtain our solution T.
It is possible to prove this theorem in three steps:
1) The Laplace equation is linear, then if T1 and T2 are solutions, also (T1-T2) is a solution: here in particular T’ and T” are solutions, then also T is;
2) The boundary conditions written above are satisfied by a T field given by (Eq 3.3);
3) Then T is a solution of our equation with these particular boundary conditions, but the solution is unique for the Uniqueness Theorem for Harmonic Functions then, T is the solution...
The base of this proof is the linearity of the grad operator, which allows the first property. But also the temporal derivative is linear, and then we have another independent fundamental result: The T field may be calculated by this way also for transient conditions, if we use the equivalent transient solutions for the T”. We are not ready to use here this corollary, probably very important. The geothermal energy focusing on caves
It is interesting to look for other consequences. Let us return to our [Eq. 3.3] to apply the grad operator (that in equation will be noted with Ñ) and multiplying for the rock conductivity KR
![]()
These terms are now the energy fluxes that flow through the systems S, S’ and S”, and then
![]()
But the energy flux in the system S’ is simply -Fgtk where k is the unit vector in the z-direction, and then
![]()
This means that we are able to calculate the energy fluxes in the system S with vectorial subtractions between the S” system, complex but already studied, and the trivial S’. If we multiply this equation by the surface element dS and integrate on a wide surface A that contains all the surroundings of the cave we have
![]()
The term F´A describes the flux outgoing from the surface in presence of the cave, Fgt´A the total flux if it would not be the cave, than the energy flux captured by the cave is the difference between the two
![]() [3.4]
[3.4]
In this way the problem of energy interception of a cold cave buried in an energy flux is reduced to the energy transfer between a hot cave and the surface.
Now it is possible to study the T” solutions, going to the heat transfer engineering to use its results.
The shape factor
The thermal transfer engineering uses a very effective approach to the problem of complex-shape systems.
Let us return back to the fundamental equation of conductivity, now written in three dimensions. The thermal flux through a surface element dA is given by
![]()
Where KR is the body (rock) conductivity. We may consider two sources at definite temperature T1 and T2. The thermal energy is drained between the two by an intermediate temperature field configuration, which depends on the system shape in an extremely complex manner.
Let us call Aiso the isothermal surfaces that we can draw between the two sources; these surfaces can be infinite, also if neither of the two bodies is infinite.
The grad (T) must be perpendicular to these surfaces because the thermal flux vector cannot have any component along an isothermal surface, and then the thermal energy flows normally to these surfaces.
Let us call n the coordinate along the thermal flow path. The previous equation gives the thermal flux as
![]()
The total flux between the two sources is then given by the integral of thermal flux on any of these surfaces. It is not important to choose one or the other, because we have assumed that the only two “heat producer or destroyer” are these two sources, and the energy must be conserved. The thermal transfer through one of these surfaces is therefore
![]()
We define now a new dimensionless temperature T* (that is in fact a relative temperature variation in the path between the two sources) as
![]()
Where T1 and T2 are the sources temperatures. Then it is possible to write
![]()
In this way the sources temperatures are analytically separated from the system geometry, which now is completely included in the last integral, which is nevertheless extremely complex also for trivial configuration.
This equation has to be compared with the usual equation which describes the thermal energy transfer between two sources separated by a uniform distance Dz through an area A
![]()
We see that the integral behaves like the ratio between A and the sources distance, and then the system geometry is included in this term
![]()
The term in brackets is the ratio between the surface crossed by the thermal energy and the distance between the two sources. It is a “length” that characterises each system shape that exchanges energy among two sources.
This scale-length is called “shape factor” in literature (Carslaw, 1959; Hahne, 1975; Holman, 1996; Ozisik and Necati, 1993; Kays, 1966). We adopt unwillingly the usual notation, that uses the “S” for a length, but we shall write SF, hoping to reduce (perhaps…) confusion with the subscript “F”. Then
![]() [3.5]
[3.5]
The geothermal power absorbed by the cave can be then written as
![]() [3.6]
[3.6]
Now we have to study the way to use this result.
The “shape factor” calculation
We do not have to study in details the way to calculate the shape factors. Still in simple configuration the isothermal surface calculation is very complex and the integration is in general extremely difficult, but the heat-exchanges literature contains many shape factors worked out for the most common geometrical configurations. Most of these results have been obtained based on advanced analytical methods (conformal mapping, superposition, special transforms, analogies with the electrical potential studies and so on); it is not useful for us here to study these approaches.
Table 2 shows these shape factors in interesting situation (Holman, 1996)
We are going to use these shape factors, but first it is necessary to answer an important question: Are the shape factors linear? Let us discuss the question with an example.
Table 2
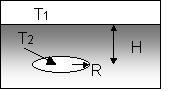
Semi-infinite medium with isothermal surface and isothermal spherical cavity of radius R at depth H |
|
|
|
Semi-infinite medium with isothermal surface and isothermal disc of radius R parallel to the surface at depth H |
|
|
|
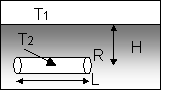
Semi-infinite medium with isothermal surface and isothermal cylindrical cavity of length L of radius R, parallel to the surface at depth H |
|
|
|
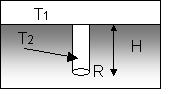
Semi-infinite medium with isothermal surface and isothermal cylindrical hole of radius R drilled to a depth H normal to the surface. |
|
|
|
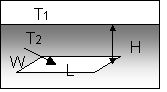
Semi-infinite medium with isothermal surface and isothermal plate (width W, long L, H>>W) parallel to the surface at depth H |
|
|
If we know the shape factors of two independent systems S1 and S2, say, one composed by two cylinders and the other of a sphere and a cylinder, can we consider a third system S3 (in this case, two cylinders and a sphere) as composed by some “sum” of the two firsts, and consider that its shape factor is given by some “sum” of the two?
Unfortunately the answer is: No, we cannot. The temperature fields are linear and then the S3 temperature field can really be calculated from the S1 and S2, but it changes completely the equipotential surfaces on which the integration is performed to “average” the flux in the integral [Eq. 3.5]. It is therefore necessary to recalculate these surfaces and to repeat the integration that will give a result that has no direct connection with the integrations of S1 and S2 fields.
This means that, for instance, the knowledge of the shape factor of a conduit buried in a semi-infinite medium tells us almost nothing about the shape factor of two parallel conduits in the same medium, unless their distance would be so large that each temperature field is not affected by the other. Only in this latter case the shape factor of the two conduits is the sum of the shape factor of two single conduits, but in general it is not so.
4. The interception of geothermal flux by caves
The geothermal cross sections of caves
It is now possible to apply the previous results to the problem of interaction between caves and geothermal flux. It is stated above that, to satisfy the boundary conditions, the T” temperature has to be
![]()
As a consequence, the equation that gives the power intercepted
![]()
It is reduced to the very simple result
![]() [4.1]
[4.1]
That is
![]()
Table 3 shows that the scale-size of shape factor is some 1-10 times larger that the scale-size of the underground structure. The last equation has to be compared with [Eq. 3.1].
Table 3
Conduit radius r [m] |
Shape factor SF [m] |
Intercepted power [J a-1] |
Average Flux on conduit [W m-2] |
|
0.01 |
165 |
1.7´1011 |
900 |
|
0.1 |
210 |
2.1´1011 |
110 |
|
0.5 |
250 |
2.5´1011 |
25 |
|
2 |
310 |
3.1´1011 |
8 |
|
5 |
360 |
3.6´1011 |
3.8 |
Therefore, the effective area (we call it “thermal cross section”) for thermal flux absorption of an underground conduit (Fig. 11) is not its geometrical area but instead SFH, roughly 10 times the cave size multiplied by its depth, then it is always enormously greater than the cave’s actual area! This amplification is due to the “converging lens” effect created by the presence of cold fluids in the cave that affects the whole structure of the rock temperature field.
Fig. 11. A deep draining conduit can create a very large geothermal shadow on the surface. Its scale size is not the conduit size, but the conduit depth.
For example, let us estimate the geothermal power intercepted by a conduit at a depth H=500 m with radius r=0.5 m and long L=300 m. We may use the shape factor given by
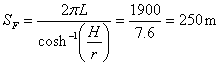
With Fgt=2´106 J m2a-1 we have
![]()
Which is really a big power. It is possible to study how much this figure changes with conduit radius. Table 3 shows the energy collected, by conduits of different sizes.
The result in the third column at first appears surprising, because it shows that the variation of the conduit size does not affect so much the intercepted power, but it is reasonable because the power is not absorbed by the conduit surface, but by the focusing effect of conduit on the temperature field.
The fourth column shows the surprisingly high average thermal flux (note that are Watt per square metre!) that enters through the conduit transverse surface. For comparison, the Sun deposits on average 1.4 kWm-2 on the Earth surface: The geothermal energy deposition on small conduits is then of the same order! This appears to be absolutely unbelievable, but is it true?
Roughly, the answer is that: Yes, it is true. But there are other important details to be taken into account.
The heating of water in deep conduits
Let us discuss the effective water heating in the focusing conduit, calling T its temperature at the springs.
In the previous discussion, it was made the fundamental assumption that the water temperature T0 in the conduit does not change and really it is its low temperature that changes the whole temperature field of surrounding rock. This is equivalent to assume that the water flux (or air flux in case of dry caves) is so large that the enthalpy intercepted by the conduit flows away in the form of a small temperature increase of a very large amount of fluid, and does not really affect the conduit temperature.
We have then that the maximum energy extraction efficiency is obtained if the exit temperature T is almost equal to T0.
We have the opposite limit, if the warming is so large that the water temperature T becomes T”, the temperature of undisturbed rock. In this case the conduit becomes completely “transparent” to the geothermal flux, the temperature field assumes a regular geothermal gradient not affected by the cave presence and, as a consequence, just a little energy is intercepted. The water into the conduit is then a hot “mine water” and the classical, “wrong” solution [Eq. 3.1] becomes correct.
The real cases are intermediate between these two extremes, because in first approximation the water really warms but, as a consequence, its capability to intercept geothermal energy is reduced, because the temperature difference between the rock and the water becomes smaller. Really the scenario is still more complex, because the water temperature increases along its path underground: It enters cool, very efficient in geothermal energy focussing, but as long as it warms downstream its capability to intercept the geothermal flux decrease. The non-linearity of SF forbids correct analytical solutions, but we can make some other step.
The critical shielding discharge
It is possible to estimate the water heating along a deep conduit and its final temperature as a function of conduit parameters.
We have just seen that two extreme scenarios are possible. If the fluid flux is very large the rock temperature field is completely changed, the geothermal energy flow interception is maximum and the water flows out at T0. At the other extreme, if the water flow is very small, the rock temperature field is completely undisturbed, the geothermal energy flow to the water is minimum and the water flows out quite hot, at T”.
Let us define the “critical fluid flux” Qc that divides these two scenarios in a usually idealised way. We look for a water flux Qc that enters at temperature T0 and flows out at T” in stationary conditions. The enthalpy subtracted to the system is
![]()
If we admit that the system parameters do not depend on time, this enthalpy deficit must be given by the incoming geothermal flux Wdt. Then using [Eq. 4.1] we have
![]()
But T” is given by
![]()
And we obtain
![]() [4.2]
[4.2]
Then the critical flux is simply the conduit shape factor “scaled” by a dimensional term (rock conductivity divided by the thermal capacity of flowing fluid). In terms of volume flux
![]()
From another point of view, Qc can be considered the critical flux below which it is possible to consider that the rock temperature field is undisturbed. Or, from still another point of view, we can be sure that a water flux much larger than Qc perturbs the rock.
The solution [Eq. 4.2], which is surprisingly simple in comparison with the bloody analytical difficulties of the problem, is able to give also the velocity that water must have to satisfy the equation. If the conduit radius is r, then
![]()
In the case of a water draining conduit in limestone we have
![]() [4.3]
[4.3]
If the conduit drains air, the critical flux becomes
![]()
The shape factor is in general comparable with the conduit length, usually some 103-104 m, therefore the water flux able to create changes in the rock temperature fields is in general quite small. Neither the air flux requested to cool the rock it is too large, in absolute, but its small thermal capacity and its very small density cause a large volume flow request.
It is nevertheless necessary to remember that temperature field changes are only possible if the fluid fluxes have had sufficient time (more than Dteq defined in [Eq. 1.1]) to converge at the stationary (equilibrium) state.
The critical flux Qc for air or water are extremely important for another reason: They are the air or water fluxes able to shadow the upper rock from the geothermal flux, forcing its temperature near to the average yearly temperature of external atmosphere, Tave.
Finally, it is important to note that this work was originally a chapter of an underground climate physics book. Its purpose was to estimate when we could consider a cave as “shielded” from the upward geothermal energy flux. If the flux is much larger than Qc we are sure that the mountain parts (and caves) above the conduit are shielded; if the flux is well below the critical value the conduit is “transparent” to the geothermal energy and we have to include also its contribution to analyse the underground climate in the rock above the conduit.
We are going to improve this point of view and discover that Qc has another, still more important, meaning.
Geothermal power intercepted
We can calculate the effective cave temperature T at the equilibrium and solve the inverse problem, the estimation of flowing depth of hot spring waters.
The final system temperature must lie between T0 (near it for high water discharges) and T” (near it for low discharges). Let us call WM the maximum power that it can be subtracted by our system
![]() [4.4]
[4.4]
Which is valuable for very large water flows and outflowing temperature around T0.
If we call T the real (unknown) conduit temperature at the equilibrium, the residual outgoing upward flux is not zero, because it “filters” an energy given by
![]()
The difference between WM and Wup is the net flux entering inside the cave from below. If the conduit is at temperature T, the energy conservation states
![]()
But from [Eq. 3.2] we have
![]()
Then
![]() [4.5]
[4.5]
If T=T0 the equation reduces to Win=WM (which describes the “system S” situation), and if T=T” the term Win vanishes, as expected.
Therefore, the geothermal flux intercepted by the cave is reduced as long as its final temperature T increases: The cave is becoming “transparent”, and this equation describes its “fading” inside the temperature field.
Temperature and deposited power versus discharge
Usually we have very small possibilities to establish a natural conduit discharge. We deal with actual discharge Q, and we can only try to understand how this water (or air) flow is affected by the geothermal flux.
Let us then return to the application of the First Principle [Eq. 4.5]; if we call Q the total actual water flux in the system, it gives
![]() [4.6]
[4.6]
Where we have assumed that the whole entering energy flux goes to warm the water flux. This statement is true if we admit that the thermal energy is released on the whole system, i.e. it is true if the temperature T, which is actually the output water temperature, can be used to describe the whole system, also in its further parts. It is a strong, and in general false, hypothesis, but it is better to assume it as true and only afterwards have a look on what happens in more real situations.
With the previous results and trivial calculations, we have
![]() [4.7]
[4.7]
This important equation relates the actual flux Q to the output temperature T in terms of the critical shielding flux Qc and the surrounding temperatures. It is very easy to solve it to obtain
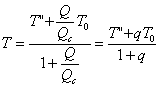 [4.8]
[4.8]
Where we have called
![]()
[4.9]
The excess temperature above the “external average” T0 is then T-T0, but its natural scale is the ratio between this difference and the theoretical, maximum difference T”-T0. Then
![]()
And calling the “excess temperature ratio” of groundwater, that is the amount of actual heating in comparison with the maximum attainable, we have
![]() [4.10]
[4.10]
With the assumption [Eq. 4.9] we can rewrite the [Eq. 4.5]
![]() [4.11]
[4.11]
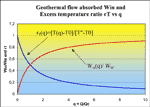
We have then two fundamental equations, [Eq. 4.10] and [Eq. 4.11], which connect the internal drainage Q to the outgoing temperature and to the intercepted geothermal flux. The two graphics (Fig. 12) describe the behaviour of the out-flowing water temperature T and of water absorbed energy as a function of discharge, obviously measured in function of our nice scale-discharge Qc (it can be adapted to air flow with trivial changes).
Fig. 12. Water temperature increase and intercepted power by a deep conduit versus water discharge.
We have previously discussed the Qc as the “shielding flux” and WM as the “maximal intercepted flux”. Now we see that they are mainly the natural scales of fluid flow and of geothermal power flux intercepted, exactly as happens with the Similarity Numbers, always a ratio between a parameter and a scale-value for it.
Really, the apparition of a natural scale-value of the main variables, the fluid flow and the geothermal power, may suggest to use this typical thermo- or fluid-physicists approach, calling the Q/Qc and W/WM terms as Someone Number, to create two underground companions to Nusselt, Reynolds, Peclet, Froude and so on Numbers.
Nevertheless we do not like this way to describe physical processes, preferring (aesthetically, because mathematically it is absolutely equivalent…) to work with the scale dimensions. Therefore we do not propose this Similarity approach although, if a name must be given to the geothermal “heat” term W/WM, we strongly suggest “Alighieri Number”...
The inverse problem
It is obviously of main interest the problem of deducing the provenance depth of a hot spring. The traditional Desio formula (Celico, 1986) assumes essentially that a water flux at temperature Tw comes from a depth H0 at which the temperature of undisturbed rock is Tw, that is
![]() [4.12]
[4.12]
This is true for “mine waters”, deposits of resident waters, which have essentially the T” temperature, but we have seen that this assumption is in general false, because a natural water flux had surely succeeded to disturb the whole rock temperature field. We have then to use [Eq. 4.8] and [Eq. 4.2] to write
![]()
That correlates the temperature increment above the local temperature to the unknown depth H, to the discharge Q and the conduit shape factor SF. Then
![]()
Comparing with [Eq. 4.12] we obtain the solution for thermally disturbed rock (Q average yearly discharge)
![]()
This solution shows that the evaluations made with the Desio formula [Eq. 4.12] are deeply underestimated, unless for very small discharges. In fact we can write
![]() [4.13]
[4.13]
It is then possible to see that the q-number is essentially the “amplification” term of estimated depth H0.
The main difficulty in these formulas it is the estimation of critical discharge Qc, which requires the knowledge of the conduit shape factor, in generally unknown. In case studies it is necessary to take into account the geological context to estimate the probable conduit shape in order to calculate the critical discharge Qc.
Let us do an example. In many case, for instance, we can assume a “U” shape for the whole drainage system. A similar conduit can simply be approximated with a conduit of length L at depth H, because its two vertical branches do not matter for the shape factor, being merged in a rock shielded by the deep drainage. Then
![]()
[4.14]
The Table 4 gives the value of inverse hyperbolic cosine term for typical conduit radius and depths.
Table 4
H↓ R→ |
0.1 m |
1 m |
10 m |
100 m |
|
200 |
8.3 |
6.0 |
3.7 |
1.3 |
|
500 |
9.2 |
6.9 |
4.6 |
2.3 |
|
2000 |
10.6 |
8.3 |
6.0 |
3.7 |
It is possible to see that, unless the nearby “pathological” cases of the last column, the denominator in [Eq. 4.14] is not far from 2π; therefore for this conduit it is possible to assume a shape factor roughly equal to its length
![]()
The formula that estimates the water provenance depth can then be approximated as
![]() [4.15]
[4.15]
In general a typical deep circuit has a very large size, many kilometres. If we call L* its length expressed in kilometres we have, for the circuit described above
![]()
And finally
![]() [4.16]
[4.16]
It is a simple formula that estimates the drainage depth as a function of discharge.
As an example, let us consider a spring with an average discharge Q=20 kg s-1, and a temperature 20°C above the local average. The depth estimation [4.12] gives H0=830 m.
If the hydro-geological context suggests a circuit length L*=20 km, the critical discharge is Qc=11 kg s-1, and then the q term is almost equal to 2. Our formula estimates then a depth H of 2.5 km for the circuit, much more than supposed…
With this value we can return to the geological context and, if we have other information (like the circulation time), to more accurate estimations of the ratio between the depth and the radius of a deep drainage system. A better estimation of provenance depth with [Eq. 4.13] and [Eq. 4.14] is then possible.
It is nevertheless better to remember that we are working with the assumption that the system has attained stationary condition; the above formula is then correct for water fluxes that persist from very long times, much longer than Dteq of [Eq. 1.1].
Temperature changes into the system
It is possible to perform a last “calibration”.
We have already noted that we are assuming that it is possible to define univocally a system temperature T, but this is not always true. It is possible to speak univocally of “system temperature” if each part of the system is uniformly heated by the energy flux, for instance if the head and the tail of water flux are mixed (for instance, when the water enters in a spherical deposit). Nevertheless this is not the usual situation because in a real conduit the water enters with a temperature T0 and flows warming up to the final temperature T.
It is possible to perform a last step, considering a long conduit L, along which the water is heated. The term T is now the temperature at the length x, in a section dx with shape factor sF. The thermal flow and the temperature increase in that section is then given by [Eq. 4.5]
![]()
And then
![]()
This is an equation that could solve the problem, if we would able to integrate the left part, but unfortunately this is not possible.
We have written sF and not dSF (as would be natural) because it is not possible to pass from the equation that gives SF as a function of L, to the contribution of a part dx of L to SF. At the end of the third chapter, we have noted that SF does not linearly depend on each dx part, because it comes from an average on the whole space and system, and it is not possible to consider it as the result of an integration on some dx.
For instance, the contribution of the dx at one conduit edge covers a cone above it, and the local sF is like that given by a small sphere, whereas the dx in the middle of conduit gives a very small contribution.
We can nevertheless integrate the last equation assuming the false approximations sF=dSF. It makes no analytical sense but it probably introduces an error smaller than the assumption of uniform system temperature. Then for a conduit buried in a semi-infinite medium at depth H
![]()
Using Qc becomes
![]()
And integrating on x from 0 to L and on T from T0 to T we have
![]()
Adding and subtracting T0 from the equation left side, we have
![]() [4.17]
[4.17]
This has to be compared with [Eq. 4.10]. It is a simple and nice equation that describes the water heating during a flow.
The Qc term has returned, and continues to be the scale discharge of deep conduits. If the effective discharge Q is large (in comparison with Qc) the water temperature at the outflow is near the T0, and if q is near 0 the T=T”.
The shape factor has disappeared, because this equation is valuable everywhere the (strong and false) sF=dSF approximation is valuable.
Nevertheless we can suppose that it is reasonable model, and we guess that the last equation gives a fair approximation of natural heating processes along a conduit.
It is useful to invert again the problem to obtain the estimated depth crossed by water of a spring at temperature Tw. We have
![]()
And with simple passages
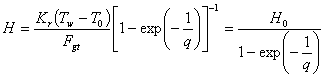
[4.18]
That corresponds to [Eq. 4.13], and reduces to it for q~0 and q>>1. With the same assumption of [Eq. 4.16] on shape factor, and L* in [km], it gives
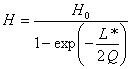
[4.19]
That can be considered a reasonable formula to estimate the water provenance depth, for water flows that have attained a steady state situation with rock.
Returning to the previous example, of a spring with Q=20 kgs-1, and a temperature 20 °C above the local average, H0=830 m, Qc=11 kg s-1, and q=2.
The corrective term to be applied to H0 with [Eq. 4.16] it is a factor 3, but now [Eq. 4.19] gives a factor 2.54.
Really the temperature variability along the conduit gives [Eq. 4.19] a final heating at a depth smaller than in the case of a “global” heating [Eq. 4.13], but the difference does not appear as too significant if compared with the intrinsic uncertainties of such problems.
Steady State Geothermal Power Plant
In the previous chapters, it has been shown implicitly a way to extract power from underground, using a deep conduit that focuses on itself large amounts of geothermal energy. This is deeply different from the usual Geothermal Power Plants, which extracts energy (or, better, are believed to extract, because cool water always focus on itself the temperature field) from hot rock, directly cooling it. In principle, when the rock is cooled the power plant stops its work.
Here we have shown that the deep cooling effect acts as an energy attractor on the cooled rock, and then that a power plant working in such way, it will never end its fuel.
We want here to make the next step, looking for its “constructive” efficiency.
Consider a fluid that transfers energy QH from a “hot” source at TH to a colder source at TL. Does this process produce work? If the energy transfer is made with “special” systems it does: They are called “thermal engines” and use the energy flow from TH to TL to produce work. A power plant is said to “produce” energy, but this is trivially false because the energy cannot be neither produced nor destroyed: It stores energy at a very low entropy (“work”) in an entropy flow from a high temperature (low entropy) to a low (high entropy).
The Second Principle of Thermodynamics states that the efficiency -that is the ratio between the work rate given L and the heat rate absorbed W- of a reversible thermal engine working between the two sources is
![]()
But we have that
![]()
And then
![]()
That is, the maximum work available is given by the product of the temperature of cold source and entropy change during cooling, which is the Free Energy variation in the transformation.
In the case of interaction cave-geothermal field, the cave acts as a thermal sink, in two phases. In the first step it intercepts a flux of geothermal energy W (low entropy, temperature T”) from downward, which results in a water temperature increase from T0 to T. In the second step the energy it is released as “disordered energy” to the atmosphere (high entropy, T0) at the spring. For instance, considering the deep conduit as a geothermal power plant, we have that its entropy production per time unit Dt -we are dealing with discharge Q- is
![]()
Calling
![]()
With some work and using [Eq. 6.1]
![]()
This shows that the entropy production goes to zero for q=0 and q=![]() , because if the water flow is very small the fluid final temperature is quite high but the total energy removed is very small; from the other side, if a lot of water flows into the conduit, its final temperature is essentially T0, then the entropy is able to flow between the rock and the water, but it is not finally transferred to the atmosphere and to an external “final user”.
, because if the water flow is very small the fluid final temperature is quite high but the total energy removed is very small; from the other side, if a lot of water flows into the conduit, its final temperature is essentially T0, then the entropy is able to flow between the rock and the water, but it is not finally transferred to the atmosphere and to an external “final user”.
It is easy to calculate the value qM for which the entropy flow attains its maximum
![]()
That we can substitute in the previous equation to obtain the maximum of entropy flow. In natural cases the term T0 is some 280 K, the T” some 350K, then the ratio is slightly more than 1, and then
![]()
Which gives, erasing the second-order terms, the maximum power production of this geothermal power plant
![]()
It is necessary to emphasize the difference between the subtracted power WM and the maximum available work (or power) LMax. The first is interesting to make some use that requires enthalpy at constant temperature, as it is the case of ice melting or water evaporation, for which WM, not LMax, is used. But to create structures we need “work” also in the physical sense: Order, available work.
Therefore, the LMax terms in each water heating and rock cooling processes are directly connected with the entropy rate at disposal for constructive processes, that is, they may appear as the building rate of ordered structures, like conduit networks.
Geothermics and phreatic conduit genesis
We have observed above that the initial purpose of this work was to show that the geothermal energy flux could not participate in the characterisation of cave climate and then, for instance, to speleogenesis (Badino, 2005).
As the reader has seen, we are showing exactly the contrary.
Here we are going to make the last step giving some ideas about the geothermal role in the genesis of phreatic conduits and in general of underwater drainage networks.
During deep flow the underground waters are warmed from their starting temperature T0 up to the final T, that has a theoretical maximum at T”, as shown above.
What is the typical temperature increase? We have seen that a conduit is able to shield the geothermal flux like a plane watertable does, then the scale temperature increase is around the value given by [Eq. 2.1]
![]()
Therefore, in real cases it is in the range between 0.2 and 3 °C, a temperature drop that water gains during flow between the cave bottom and the springs. Now we know that this temperature change happens also along conduits, not only in the “watertable”, and that the power release is concentrated on the conduit surface walls. How does this warming affect the water chemistry?
We can outline the chemical behaviour of water saturated of calcium carbonate entering in flooded conduits.
It is well known that the carbonate dissolution in water is very complex (Snoeyink, 1980; Ford and Williams, 1989; Dreybrodt, 2000) because the equilibrium state results from the combined equilibriums of different, interconnected reactions, which depends on temperature, local pH and the presence of other dissolved salts with common ions.
In the simplest case, the first equilibrium reaction gives the amount of dissolved carbon dioxide, for which in usual conditions the Henry Law holds, stating that the dissolved gas decreases with temperature and it is proportional to its partial pressure above the water surface. Therefore, its quantity depends also on the kinetics of gas transport until the surface, if it does exist.
The other reactions, which involve only water and carbon dioxide, are the dissociation of carbonic acid in calcium bicarbonate and H+, the dissociation of bicarbonate and the equilibrium H+ and OH- in water. These dissociations tend to increase with temperature thanks to the increase of available energy.
The last main reaction describes the equilibrium between the calcium carbonate and water enriched with carbon dioxide. The carbonate dissolution releases ions that are in part the same already present in water.
This complex system forces to find the solution of many different equations describing equilibrium kinetics, charge and mass conservation. General solution charts are given in (Ford and Williams, 1989); they show the saturation values at the equilibrium for various initial partial carbon dioxide pressures. It results that in open systems (with release of carbon dioxide excesses) the warming of a calcite saturated water gives, without exceptions, a super-saturation and then provokes a calcite, or aragonite, deposition.
In a closed system this behaviour changes in a complex way. Generally a super-saturation is produced, but if the initial CO2 partial pressure is below 200 Pa (0.002 atm) and the temperature is below 30 °C, a calcite under-saturation appears as result of water heating, as larger as colder is the water.
The typical carbon dioxide partial pressure in free atmosphere is 3.5x10-4 atm, then at 10 °C the calcite equivalent content at the saturation is around 12 mg l-1. A water temperature increase of 1 °C result in a saturation value of 0.02-0.04 mg larger, i.e. with a flux of 1 m3s-1 it gives around 103 kg of dissolved rock per year.
It is a small figure but it suggests that further studies are necessary to a more complete understanding of saturation conditions as a function of temperature, of chemically complex waters in a closed system.
In any case indirect evidences of effectiveness of speleogenetic processes induced by geothermal heating in phreatic conduits can be found, because if these processes are possible, they have to affect the network morphologies:
1) the geothermal energy is released only in the lowest conduit walls, then the dissolving characteristics have to depend on the rock surface orientation;
2) a deep conduit shadows completely the upper rock, then the formation of a conduit that cross the rock above another is hampered, and this affects the whole drainage conduit structure.
Similar processes can probably play a part also in the deep drainage network formation in glaciers (Badino, 2002), but either ice or limestone, a lot of work has still to be done for a better understanding of geothermal role in karst.
Conclusions
The estimations of temperature fields inside mountains are important for speleogenesis and for underground climate studies, but also for many cases which require an energy balance on a sub-geological time-scale, like glacier stability, geothermal spring studies, deep hydro-geological analysis, tunnel drilling and so on.
We have shown that these potentially cumbersome modelling can be reduced to simple calculations that allow quite accurate estimations of energy absorbed by deep structures and of provenance depths of geothermal waters.
These results could also be applied for remote sensing of deep drainage structures and for construction of inexhaustible geothermal power plants, but at present these applications appear to meet insurmountable practical difficulties.
References
- AA. VV., 2004. Under the Desert: the Mysterious Water of Cuatro Ciénegas. La Venta.
- Badino G. 1995. Fisica del Clima Sotterraneo. Memorie IIS 7, II.
- Badino G. 2000. I Gradienti di Temperatura nei Monti, un Indicatore Esplorativo. Talp-FST 21, 72-80
- Badino G. 2002. The Glacial Karst. Proc. of V Int. Symp. on Glacier Caves and Cryokarst 2000, Nimbus 23, VII, 1/2002.
- Badino G. 2004. Cave Temperatures and Global Climatic Change. Int. J. Speleol. 33.
- Badino G. and Forti, P. 2005. L’eccezionale Ambiente della Cueva de los Cristales. Proc. “Le Grotte di Miniera”, Memorie IIS XVII, II.
- Badino G. 2005. Clouds in Caves. Speleogenesis and Evolution of Karst Aquifers 2 (2), www.speleogenesis.info.
- Badino G. 2005. Nuovo Collegamento Ferroviario Torino-Lione, Temperature del Tunnel di Bussoleno, Geodata, Torino, unpubl.
- Balcerzak M. and Raynor S. 1961. Steady State Temperature Distribution and Heat Flow in Prismatic Bars”, Int. J. Heat Mass Transfer 3: 113-125,
- Bejan A. 1993. Heat Transfer. John Wiley and Sons.
- Benderitter Y., Roy B. and Tabbagh A. 1993 Flow Characterization through Heat Transfer: Evidence in a Carbonate Fractured Medium. Wat. Res. Res. 29, 11: 3741-3747.
- Bohren C. and Albrecht B. 1998. Atmospheric Thermodynamics. Oxford Un. Press, 402 pp.
- Bogli A. 1980. Karst Hydrology and Physical Speleology. Springer-Verlag.
- Carslaw H. and Jaeger J. 1959. Conduction of Heat in Solids, Oxford-Clarendon Press.
- Catalano P. 1993. Laboratori Sotterranei: Relazione Geologica. Unpublished, INFN.
- Celico P. 1986. Prospezioni Idrogeologiche. Liguori.
- Dreybrodt W. 2000. Equilibrium Chemistry of Karst Water in Limestone Terranes. In Speleogenesis: Evolution of karst aquifers, Klimchouk, A., Ford, D.C., Palmer, A.N., and Dreybrodt, W. (Eds.), Nat. Speleol. Soc., USA: 130-135.
- Ford D. and Williams P. 1989. Karst Geomorphology and Hydrology, Unwin Hyman.
- Goy L., Fabre D. and Menard G. 1996. Modelling of Rock Temperatures for Deep Alpine Tunnel Projects. Rock Mech. Rock Engng 29.
- Guichonnet P. 1967. Il Traforo del Monte Bianco, Mondadori.
- Hahne E. and Grigull U. 1975. Formfaktor und Formwiderstand der Stationaren Mehrdimensionalen Warmeleitung, Int. J. Heat Mass Transfer 18: 751-767
- Holman J. 1996. Heat Transfer, MacGraw-Hill.
- Isachenko V., Osipova V. and Sukomel A. 1969. Heat Transfer, MIR.
- Jeannin P., Liedl R. and Sauter M. 1997. Some Concepts about Heat Transfer in Karstic Systems. 195-198.
- Kays W. 1966. Convective Heat and Mass Transfer. McGraw-Hill.
- Lee et al. 1966. Heat Flow and Volcanic Temperatures. Handbook of Physical Constants, The Geological Society of America.
- Koenigsberger J. and Thoma E. 1906. Uber die Beeinflussung der geothermischen Tiefenstufe durch Berge und Taler. Eclog. Geol. Helv. IX (1).
- Laidler K. and Meiser J. 1995 Physical Chemistry. Houghton-Mifflin Co.
- Lismonde B. 2002. Aérologie des Systèmes Karstiques. CDS Isére.
- Luetscher M. and Jeannin P.-Y. 2004. Temperature distribution in karst systems: the role of air and water fluxes. Speleogenesis and Evolution of Karst Aquifers 2 (2), (from Terra Nova 16):, 344–350
- Nashchokin V. 1979. Engineering Thermodynamics and Heat Transfer. Mir, 573 pp.
- Ozisik M. and Necati. 1993. Heat Conduction,.Wiley InterScience.
- Schoeller H. 1962. Les eaux souterraines. Masson.
- Snoeyink V.and Jenkins D. 1980. Water Chemistry. John Wiley & Sons.
- Szechy K. 1973. The Art of Tunnelling, Akademiai Kiado, Budapest.
- U.S. Bureau of Mines. 1996. Dictionary of Mining, Mineral, and Related Terms, CD-ROM.
- Verhoogen J. 1956. Temperatures within the Earth. In Physics and Chemistry of the Earth, Pergamon Press, I.